La experiencia y la repetición influyen en la eficiencia de los procesos. En tareas intensivas en mano de obra, como montajes, es importante conocer el efecto de la curva de aprendizaje. En este artículo desglosaremos este concepto y mostraremos cómo su comprensión puede agilizar la manera en que las empresas mejoran su rendimiento y competitividad.
INDICE
1.- INTRODUCCIÓN Y CONCEPTOS.
1.1.- Antecedentes y objeto del proyecto.
1.2.- Conceptos previos.
2.- FUNDAMENTOS TEÓRICOS (INGENIERÍA ECONÓMICA).
2.1.- Introducción al aprendizaje y la mejora.
2.2.- Fórmula de cálculo de la curva de aprendizaje.
2.3.- Ejemplo 1. Diseño y montaje de coches de carreras.
2.4.- Ejemplo 2. Fabricación de viviendas.
3.- FUNDAMENTOS TEÓRICOS (INGENIERÍA INDUSTRIAL).
3.1.- Estándares temporales.
3.2.- La curva de aprendizaje.
3.3.- Tasas típicas para curva de aprendizaje.
4.- CONCLUSIONES.
1.- INTRODUCCIÓN Y CONCEPTOS.
1.1.- Antecedentes y objeto del proyecto.
La experiencia y la repetición influyen en la eficiencia de los procesos. En tareas intensivas en mano de obra, como montajes, es importante conocer el efecto de la curva de aprendizaje. En este artículo desglosaremos este concepto y mostraremos cómo su comprensión puede agilizar la manera en que las empresas mejoran su rendimiento y competitividad.
1.2.- Conceptos previos.
La medición de tiempos estándar es un proceso esencial en la industria para establecer objetivos de producción y medir el rendimiento de las operaciones. Sin embargo, a lo largo del tiempo, la eficiencia de las operaciones puede cambiar debido a varios factores, como la experiencia de los trabajadores, la introducción de nuevas tecnologías y equipos, cambios en el diseño del producto, entre otros. Por lo tanto, es recomendable revisar y actualizar los tiempos estándar de las operaciones para garantizar la productividad y la rentabilidad.
El concepto de curva de aprendizaje es fundamental para entender por qué es necesario revisar y actualizar los tiempos estándar de las operaciones. La curva de aprendizaje se refiere a la relación entre el tiempo y la tasa de aprendizaje. A medida que los trabajadores adquieren experiencia y práctica en una tarea en particular, el tiempo requerido para completar la tarea disminuye, lo que resulta en una tasa de aprendizaje más alta.
La fórmula de la curva de aprendizaje muestra que a medida que la cantidad de unidades producidas aumenta, el tiempo requerido para completar la tarea disminuye. Sin embargo, la curva de aprendizaje eventualmente se aplana, lo que indica que la tasa de aprendizaje ha disminuido.
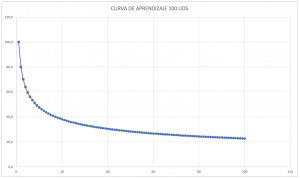
Esto sugiere que los tiempos estándar de las operaciones deben revisarse luego de la puesta en marcha de un nuevo proceso o método, teniendo en cuenta la curva de aprendizaje.
2.- FUNDAMENTOS TEÓRICOS (INGENIERÍA ECONÓMICA).
Se presentan a continuación extractos y recomendaciones del siguiente libro:
- Sullivan, Wicks y Luxhoj, “Ingeniería Económica”, Pearson Educación. 12 edición. 2004.
Las fórmulas se simplifican y los ejemplos se amplían para su mejor comprensión.
2.1.- Introducción al aprendizaje y la mejora.
“Una curva de aprendizaje es un modelo matemático que explica el fenómeno del aumento de la eficiencia de un trabajador y de la mejora del rendimiento de una organización a partir de la producción repetida de un producto o servicio. A la curva de aprendizaje a veces se le llama curva de experiencia, o función del progreso de la manufactura; en lo fundamental, se trata de una relación de estimación. El primer lugar en que se observó la curva de aprendizaje (mejora) fue en las industria aérea y aeroespacial, con respecto a las horas de trabajo por unidad. Sin embargo, se aplica a muchas situaciones diferentes. Por ejemplo, el efecto de la curva de aprendizaje se utiliza en la estimación de horas profesionales que dedica un equipo de ingeniería a la realización de diseños detallados sucesivos dentro de una familia de productos, así como para estimar las horas de trabajo que se requieren para ensamblar automóviles.
El concepto básico de las curvas de aprendizaje es que algunos de los insumos (por ejemplo, costos de la energía, horas de trabajo, costos de material, horas de ingeniería) disminuyen por unidad de salida, conforme se incrementa el número de unidades.
La mayoría de las curvas de aprendizaje se basan en el supuesto de que ocurre una reducción porcentual constante en, por ejemplo, las horas de trabajo, conforme el número de unidades producidas se duplica. De esta forma, si se necesitan 100 horas de trabajo para producir la primera unidad y se supone una curva de aprendizaje del 90%, entonces se requerirán 100*(0,9) = 90 horas de trabajo para producir la segunda unidad. En forma similar, se necesitarán 100*(0,9)2 = 81 horas de trabajo para producir la cuarta unidad; 100*(0.9)3 = 72,9 horas para producir la octava; y así sucesivamente. Por lo tanto, una curva de aprendizaje del 90% ocasiona una reducción del 10% en las horas de trabajo cada vez que se duplica la cantidad que se produce.”
P. Wright, “Factors Affecting the Cost of Airplanes”, Journal of Aeronautical Sciences, vol. 3, núm. 4. 1936.
Sullivan, Wicks y Luxhoj, “Ingeniería Económica”, Pearson Educación. 12 edición. 2004. Pág. 332.
2.2.- Fórmula de cálculo de la curva de aprendizaje.
“La suposición de que ocurre una reducción porcentual constante en la cantidad de un recurso que se emplea (por unidad de salida), cada vez que se duplica el número de unidades producidas, permite construir un modelo matemático para la función de aprendizaje (mejora). Sean:
u = número de unidades de salida,
Zu = número de unidades del insumo necesario para producir la unidad de salida número u,
K = número de unidades de insumo que se requieren para producir la primera unidad de salida,
s = parámetro de pendiente de la curva de aprendizaje, expresado en forma decimal (para una curva de aprendizaje del 90%, s = 0,9).”
Entonces,
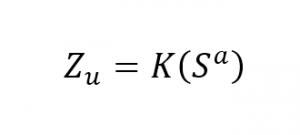
donde a = 0, 1, 2, 3, …
Así,
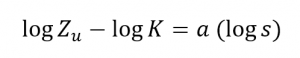
Como u = 2a
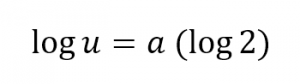
O bien, aplicando antilogaritmos, podemos obtener la siguiente simplificación:
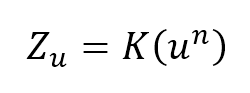
Donde
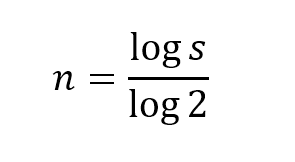
Sullivan, Wicks y Luxhoj, “Ingeniería Económica”, Pearson Educación. 12 edición. 2004. Pág. 333.
2.3.- Ejemplo 1. Diseño y montaje de coches de carreras.
Sullivan, Wicks y Luxhoj, “Ingeniería Económica”, Pearson Educación. 12 edición. 2004. Pág. 334.
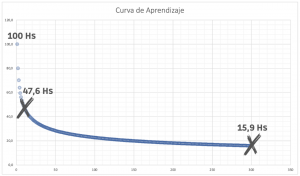
El departamento de Ingeniería Mecánica tiene un equipo de estudiantes para diseñar un auto de carreras para una competencia nacional. El tiempo que necesitó el equipo para ensamblar el primer coche fue de 100 horas. Su mejora (o tasa de aprendizaje) es de 0,8, lo que significa que cada vez que se duplica su salida, el tiempo de ensamble se reduce en un 20%. Utilice esta información para determinar el tiempo que tomará al equipo ensamblar el décimo coche.
SOLUCIÓN
A partir de la ecuación final alcanzada en el apartado anterior, y suponiendo una disminución proporcional en el tiempo de ensamble de las unidades de salida entre las cantidades duplicadas, se tiene que:
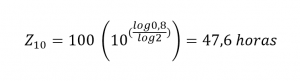
Gráficamente, quedaría como sigue:
2.4.- Ejemplo 2. Fabricación de viviendas.
Sullivan, Wicks y Luxhoj, “Ingeniería Económica”, Pearson Educación. 12 edición. 2004. Pág. 335.
La Betterbilt Construction Company diseña y construye viviendas residenciales unifamiliares. El gerente de compras de la empresa ha desarrollado una estrategia con la que todos los materiales de construcción para una casa se compran a un solo gran proveedor, pero se organiza un concurso entre unas cuantas compañías para seleccionar al proveedor para cada vivienda.
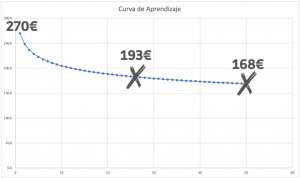
La compañía está a punto de construir, en secuencia, 16 casas nuevas de 240 metros cuadrados cada una. Se usará el mismo diseño básico, con cambios sin importancia, para todas. La oferta ganadora por los materiales de construcción para la primera residencia es de 64,800 €, que es igual a 270€ por metro cuadrado. El gerente de compras cree que, con base en experiencias anteriores, es posible emprender varias acciones para reducir el costo de los materiales en un 8% cada vez que se duplique el número de viviendas. Con base en esta información, ¿Cuál es el costo estimado de los materiales por metro cuadrado para la última (decimosexta) residencia?
SOLUCIÓN
Volviendo a hacer uso de la ecuación anterior, obtenemos:
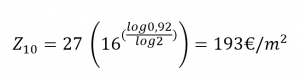
Gráficamente, quedaría como sigue:
3.- FUNDAMENTOS TEÓRICOS (INGENIERÍA INDUSTRIAL).
Se presentan a continuación extractos y recomendaciones del siguiente libro:
- Niebel y Freivalds. “Ingeniería Industrial. Métodos, estándares y diseño del trabajo”. Mc Graw Hill. 12 edición. 2009.
3.1.- Estándares temporales.
“Los empleados requieren tiempo para lograr el dominio de cualquier operación nueva o diferente. Con frecuencia, los analistas del estudio de tiempos establecen un estándar en una operación más o menos nueva, para la que no existe un volumen suficiente para que el operario alcance la eficiencia más alta. Si el analista basa la calificación del operario en los conceptos usuales de producción (es decir, la calificación del operario por debajo de 100), el estándar que resulta puede parecer demasiado estricto y es probable que el operario no pueda obtener incentivos.
Quizás el método más satisfactorio para manejar estas situaciones es la emisión de estándares temporales. El analista establece el estándar considerando la dificultad del trabajo asignado y el
número de piezas que se van a producir. Después, mediante el uso de una curva de aprendizaje para el trabajo, así como los datos estándar existentes, el analista puede desarrollar un estándar temporal equitativo para la tarea. El estándar resultante será mucho más liberal que si la tarea involucrara un alto volumen. Cuando se libera para el piso de producción, el estándar se marca claramente como “temporal” e incluye la cantidad máxima para la cual se aplica. Cuando se liberan
estándares temporales, deben tener efecto sólo por la duración del contrato, o durante 60 días, lo que ocurra primero. Al expirar, deben ser sustituidos por estándares permanentes.”
Niebel y Freivalds. “Ingeniería Industrial. Métodos, estándares y diseño del trabajo”. Mc Graw Hill. 12 edición. 2009. Pág. 346.
3.2.- La curva de aprendizaje.
“Los ingenieros industriales, los ergonomistas y otros profesionales interesados en el estudio del comportamiento humano reconocen que el aprendizaje depende del tiempo. Incluso el dominio de la operación más sencilla puede tomar horas. El trabajo complicado puede tomar días o semanas antes de que el operario logre la coordinación mental y física que le permitan pasar de un elemento a otro sin duda o demora. Este periodo y el nivel relacionado de aprendizaje forman la curva de aprendizaje, que, gráficamente, se presenta en la siguiente figura:
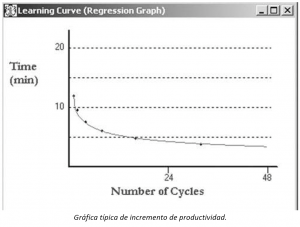
Una vez que el operario alcanza la parte más plana de la curva, se simplifica el problema de calificar el desempeño. Sin embargo, no siempre es conveniente esperar tanto para desarrollar un estándar. Los analistas pueden necesitar establecer el estándar en la parte inicial del proceso, donde la pendiente de la curva es mayor. En tales casos, resulta útil disponer de curvas de aprendizaje representativas de los diversos tipos de trabajo que se realizan. Esta información se puede usar tanto para determinar el punto en el tiempo en que sería deseable establecer el estándar, como para proporcionar una guía del nivel de productividad esperado de un operario promedio.”
Niebel y Freivalds. “Ingeniería Industrial. Métodos, estándares y diseño del trabajo”. Mc Graw Hill. 12 edición. 2009. Pág. 527.
3.3.- Tasas típicas para curva de aprendizaje.
“La teoría de la curva de aprendizaje sostiene que cuando se duplica la cantidad total de unidades producidas, el tiempo por unidad disminuye en un porcentaje constante. Por ejemplo, si los analistas esperan una tasa de aprendizaje de 80%, cuando se duplica la producción, el tiempo promedio por unidad disminuye 20%.”
Las tasas típicas de aprendizaje son las siguientes:
- Trabajo grande o fino de ensamble (como el de aviones), 70 a 80%.
- Soldadura, 80 a 90%.
- Maquinado, 90 a 95%.
Contrario a la intuición, 70% es la tasa más alta de aprendizaje, característica de todas las operaciones manuales, mientras que 100% no representaría ningún tipo de aprendizaje en el caso de las operaciones completamente automatizadas.”
Niebel y Freivalds. “Ingeniería Industrial. Métodos, estándares y diseño del trabajo”. Mc Graw Hill. 12 edición. 2009. Pág. 528.
4.- CONCLUSIONES.
En base a la metodología de la curva de aprendizaje y los ejemplos expuestos, podemos concluir lo siguiente:
- La curva de aprendizaje demuestra que a medida que los trabajadores adquieren experiencia y práctica en una tarea, el tiempo requerido para realizar esa tarea disminuye. Esto se debe a la mejora en las habilidades y conocimientos en el proceso de trabajo.
- La curva de aprendizaje es una herramienta útil para predecir y estimar los tiempos de producción futuros, especialmente cuando se trata de tareas que están siendo realizadas por primera vez. Permite establecer expectativas realistas sobre los tiempos de producción y ayuda en la planificación y programación de los procesos de trabajo.
- La medición y actualización regular de los tiempos estándar de producción basados en la curva de aprendizaje son esenciales para garantizar la eficiencia y la optimización de los procesos de trabajo. Esto permite identificar oportunidades de mejora, establecer metas realistas, asignar recursos adecuados, realizar un cálculo de costos objetivo coherentes y optimizar la asignación de tareas y tiempos de producción.
- La curva de aprendizaje también proporciona información valiosa para la toma de decisiones relacionadas con la contratación, capacitación y asignación de personal. Permite evaluar el desempeño de los trabajadores y determinar cuánto tiempo se requerirá para que alcancen un nivel de producción óptimo.
En resumen, la curva de aprendizaje justifica la necesidad de medir y actualizar los tiempos estándar de producción en las fábricas y es una herramienta clave para cualquier empresa que busca mejorar continuamente sus operaciones.