Eliminación de un cuello de botella en una empresa de laminados del metal a partir de un estudio de tiempos y su aplicación en un MRP II.
Antecedentes
A continuación, se relata un caso en el que quedará patente como la mayor de las sutilezas y pequeñeces pueden hacer cerrar una fábrica (o casi, si no se actúa a tiempo).
El caso de estudio es de una empresa que tenía el cierre pisándole los talones y tomaron la medida de urgencia de intentar resolver la situación por medio de un estudio de tiempos. Esa era la necesidad que la dirección creía tener, pero, una vez analizada la situación, Zadecon vio el problema que aquejaba a esta empresa, es decir, los cuellos de botella.
Definición del problema
La factoría que arrastraba tantos problemas se dedica a la laminación de perfiles en frío a partir de bobinas. Se enfrentaba al cierre por motivos de improductividad, los ratios de Toneladas/Hora·hombre eran muy malos comparativamente con otras factorías del mismo grupo.
La dirección se sentía totalmente impotente ya que observaba un empeño apto por parte de los operarios. Estos, a su vez, sentían el miedo del cierre y querían colaborar para mejorar la situación.
Proyecto desarrollado
Por tanto, la empresa se decidió por la mejora realizando un estudio de tiempos, por medio del estudio de tiempos se calcularía la capacidad de la industria para producir.
La necesidad de la empresa era de una fabricación de 50 Toneladas al día, para conseguir esta producción, los operarios realizaban jornadas de hasta 12 horas. El pago de estas horas extras elevaba los costes y devolvía malos datos de productividad a la dirección.
Se hizo un estudio de tiempos de cada una de las tareas y un CRP en el que se calculaba la cantidad de horas que se necesitaban al día para una producción de 50 Toneladas y 10 Operarios. El resultado fue sorprendente según el CRP se necesitaban 6 Horas de trabajo para esa producción. Revelar o comunicar esa información era algo muy delicado y que obligaba a meditar, reflexionar y revisar, antes de nada. Se revisó y, efectivamente, se necesitaban jornadas de 6 Horas para hacer el trabajo que era necesario.
El tiempo estándar de la tonelada fabricada era de un total de 1,2 H.h (Horas hombre). Por tanto, la duración necesaria a actividad normal será de: 50 Tn x 1,2 Hh/tn / 10 Hombres = 6 Horas.
Reflexionando acerca del asunto se estudió sí podrían ser limitantes las máquinas de proceso y no la mano de obra. Según el estudio, las máquinas no eran el limitante.
Sólo quedaba pensar en una posible máquina como limitante, el medio de transporte interno, el puente grúa. Para ello, se tomó el estudio de tiempos desglosado y se anotó al lado de cada tarea si era necesario puente grúa para su ejecución, ver cuadro de análisis de tiempos:

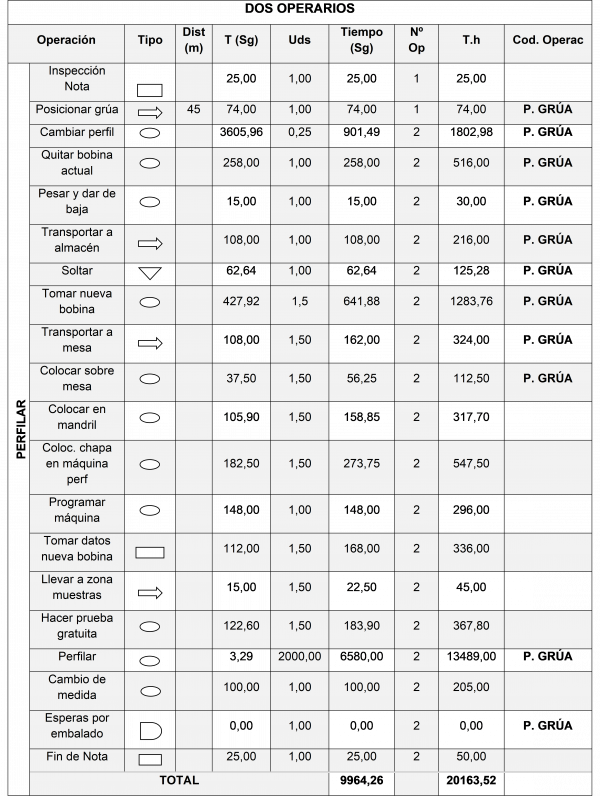
Como se puede observar, se trabaja con un nuevo parámetro, el Tiempo-Puente Grúa, que para la investigación pasa a ser más relevante que el Tiempo-hombre. El Tiempo·Puente es de 0,24 Horas/Tn.
Al conseguir este nuevo ratio calculamos cual debía ser la jornada del puente grúa para conseguir la producción que había que hacer: ¡Efectivamente! 12 Horas de trabajo. Tiempo Necesario (horas) = 50 Tn x 0,24 Horas/Tn = 12 Horas.
Por la cantidad de tareas para las que se empleaba el puente grúa y para la producción de 50 Tn al día, se necesitaban 12 Horas. Esto significa que cada uno de los operarios, tenía 6 horas de demoras diarias a causa de las esperas al puente grúa.
Esto quiere decir que los 10 Operarios tenían el doble de capacidad que un puente grúa. Existía un claro desequilibrio que había que resolver:
- Se podía mantener un puente grúa y reducir a la mitad la capacidad de los operarios, es decir, despedir a la mitad, de tal manera que no se produjesen esperas. Esto provocaba un problema social ya que significaba 5 despidos, pero bueno, al menos, la empresa sobreviviría. Por otra parte, no resuelve el problema de las jornadas de 12 horas.
- O duplicar la capacidad de puentes grúa a partir de la adquisición de uno nuevo. Esto significaría que a las 6 horas de trabajo se terminaría la jornada. El departamento comercial debería trabajar con mayor empeño para conseguir todo el trabajo que haría falta ahora, ya que quedarían 2 horas de cada jornada sin trabajo.
Finalmente, se optó por la solución 2, ¿Cuánto tendremos que producir diariamente para saturar los medios de producción disponibles actualmente? Ahora se fijan las variables jornada y número de empleados.
Producción Jornada 8 Horas (Tn) = 8 Horas x 10 Hombres / 1,2 Hh/Tn = 66,67 Toneladas.
Duración Jornada de los Puentes Grúa (Horas) = 66,67 Tn x 0,24 Horas – Puente Grúa/Tn / 2 Puentes Grúa = 8 Horas.
A esta mejora se sucedió otro problema social, la no remuneración de horas extras, lo cual generó más de un conflicto pero que poco a poco se fue resolviendo.
Capacidades adquiridas por el cliente
- Identificación de los cuellos de botella
- Liberación del cuello de botella.
- Formación de los empleados.
Beneficios del proyecto
A fecha de hoy se puede decir que la factoría en cuestión sigue abierta, mantiene el empleo y es de las más productivas del grupo.
La lección que se obtiene de este análisis y ejemplo es que acerca de los equilibrados y dimensionamientos de la fábrica, no se puede obviar nada y que la sutileza más mínima nos puede provocar grandes mejoras.
No debemos perder de vista jamás el peso que los transportes internos tienen sobre la productividad de la fábrica. Tengamos algo claro, los transportes internos, aunque no lo parezca, trabajan en cadena con el resto de los puestos y, si estos son insuficientes, pueden provocar un cuello de botella a toda la fábrica. Estudiaremos todas y cada una de las máquinas de la planta para ver qué es lo que está pasando y nos volveremos locos porque no hallamos la causa del problema, porque todo debería funcionar correctamente, en ese caso:
¡ANALICEMOS LOS TRANSPORTES INTERNOS!
Como se puede comprobar, la capacidad no puede ser estudiada solo a través de la mano de obra, sino también para las máquinas que intervienen en el proceso.